Skip to content
Submitted
- Doyoon Kim and Junbin Song. Trace Regularity PINNs: Enforcing
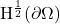 for Boundary Data. Submitted.
for Boundary Data. Submitted.
- Hongjie Dong, Pilgyu Jung, and Doyoon Kim.
 -estimates of the conormal derivative problem for parabolic equations with time measurable coefficients and
-estimates of the conormal derivative problem for parabolic equations with time measurable coefficients and 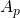 -weights. Submitted.
-weights. Submitted.
Published
- Pilgyu Jung and Doyoon Kim.
 -estimates for parabolic equations in divergence form with a half-time derivative. (https://authors.elsevier.com/a/1lH0Z_W4cPkNh) JDE, 443 (2025), 113560.
-estimates for parabolic equations in divergence form with a half-time derivative. (https://authors.elsevier.com/a/1lH0Z_W4cPkNh) JDE, 443 (2025), 113560.
- Doyoon Kim and Kwan Woo. Sobolev spaces and trace theorems for time-fractional evolution equations. Potential Analysis, 63 (2025), 1289–1333.
- Jongkeun Choi and Doyoon Kim. Green functions for stationary Stokes systems with conormal derivative boundary condition in two dimensions. Mathematische Nachrichten, 297 (2024), no.5, 1712–1736.
- Doyoon Kim, Kyeong-Hun Kim, and Kwan Woo. Trace theorem and non-zero boundary value problem for parabolic equations in weighted Sobolev spaces. Stochastics and Partial Differential Equations: Analysis and Computations, , 12 (2024), no.1, 134–172.
- Hongjie Dong and Doyoon Kim. Time fractional parabolic equations with partially SMO coefficients. JDE, 377 (2023), 759–808.
- Hongjie Dong, Pilgyu Jung, and Doyoon Kim. Boundedness of non-local operators with spatially dependent coefficients and
 -estimates for non-local equations. CVPDE, 62 (2023), no.2, Paper No.62, 28 pp.
-estimates for non-local equations. CVPDE, 62 (2023), no.2, Paper No.62, 28 pp.
- Hongjie Dong, Doyoon Kim, and Tuoc Phan. Boundary Lebesgue mixed-norm estimates for non-stationary Stokes systems with VMO coefficients. CPDE, 47 (2022), no.8, 1700–1731.
- Doyoon Kim, Kyeong-Hun Kim, and Kijung Lee. Parabolic systems with measurable coefficients in weighted Sobolev spaces. CPAA, 21 (2022), no.8, 2587–2613.
- Doyoon Kim, Seungjin Ryu, and Kwan Woo. Parabolic equations with unbounded lower-order coefficients in Sobolev spaces with mixed norms. J. Evol. Equ., 22 (2022). no.1, Paper No.9, 40 pp.
- Hongjie Dong and Doyoon Kim. Time fractional parabolic equations with measurable coefficients and embeddings for fractional parabolic Sobolev spaces. IMRN, 2021 (2021), no.22, 17563–17610.
- Hongjie Dong and Doyoon Kim. An approach for weighted mixed-norm estimates for parabolic equations with local and non-local time derivatives. Adv. Math., 377 (2021), Paper No.107494, 44 pp.
- Hongjie Dong and Doyoon Kim.
 -estimates for time fractional parabolic equations in divergence form with measurable coefficients. JFA, 278 (2020), no.3, 108338, 66 pp.
-estimates for time fractional parabolic equations in divergence form with measurable coefficients. JFA, 278 (2020), no.3, 108338, 66 pp.
- Doyoon Kim and Seungjin Ryu. The weak maximum principle for second-order elliptic and parabolic conormal derivative problems. CPAA, 19 (2020), no.1, 493–510.
- Hongjie Dong and Doyoon Kim.
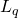 -estimates for stationary Stokes system with coefficients measurable in one direction. (http://rdcu.be/GCJ1) Bull. Math. Sci., 9 (2019), no.1, 1950004, 30 pp.
-estimates for stationary Stokes system with coefficients measurable in one direction. (http://rdcu.be/GCJ1) Bull. Math. Sci., 9 (2019), no.1, 1950004, 30 pp.
- Jongkeun Choi and Doyoon Kim. Weighted
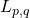 -estimates for higher order elliptic and parabolic systems with BMO
-estimates for higher order elliptic and parabolic systems with BMO coefficients on Reifenberg flat domains. (https://rdcu.be/bAY4C) CVPDE, 58 (2019), no.3, Paper No.90, 29 pp.
coefficients on Reifenberg flat domains. (https://rdcu.be/bAY4C) CVPDE, 58 (2019), no.3, Paper No.90, 29 pp.
- Jongkeun Choi and Doyoon Kim. Estimates for Green functions of Stokes systems in two dimensional domains. J. Math. Anal. Appl., 471 (2019), no.1-2, 102–125.
- Hongjie Dong and Doyoon Kim.
 -estimates for time fractional parabolic equations with coefficients measurable in time. Adv. Math., 345 (2019), 289–345.
-estimates for time fractional parabolic equations with coefficients measurable in time. Adv. Math., 345 (2019), 289–345.
- Jongkeun Choi, Hongjie Dong, and Doyoon Kim. Green functions of conormal derivative problems for stationary Stokes system. (https://rdcu.be/3b1D) J. Math. Fluid Mech., 20 (2018), no.4, 1745–1769.
- Hongjie Dong and Doyoon Kim. On
 -estimates for elliptic and parabolic equations with
-estimates for elliptic and parabolic equations with 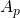 weights. Trans. Amer. Math. Soc., 370 (2018), no.7, 5081–5130.
weights. Trans. Amer. Math. Soc., 370 (2018), no.7, 5081–5130.
- Jongkeun Choi, Hongjie Dong, and Doyoon Kim. Conormal derivative problems for stationary Stokes system in Sobolev spaces. DCDS-A, 38 (2018), no.5, 2349–2374.
- Hongjie Dong and Doyoon Kim. Weighted
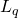 -estimates for stationary Stokes system with partially BMO coefficients. JDE, 264 (2018), no.7, 4603–4649.
-estimates for stationary Stokes system with partially BMO coefficients. JDE, 264 (2018), no.7, 4603–4649.
- Doyoon Kim, Hongjie Dong, and Hong Zhang. Neumann problem for non-divergence elliptic and parabolic equations with BMO
 coefficients in weighted Sobolev spaces. DCDS-A, 36 (2016), no.9, 4895–4914.
coefficients in weighted Sobolev spaces. DCDS-A, 36 (2016), no.9, 4895–4914.
- Sungwon Cho, Hongjie Dong, and Doyoon Kim. Boundary value problems for parabolic operators in a time-varying domain. CPDE, 40 (2015), no.7, 1282–1313.
- Hongjie Dong and Doyoon Kim. Elliptic and parabolic equations with measurable coefficients in weighted Sobolev spaces. Adv. Math., 274 (2015), 681–735.
- Hongjie Dong and Doyoon Kim. On the impossibility of
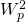 estimates for elliptic equations with piecewise constant coefficients. JFA, 267 (2014), no.10, 3963–3974.
estimates for elliptic equations with piecewise constant coefficients. JFA, 267 (2014), no.10, 3963–3974.
- Hongjie Dong and Doyoon Kim. Parabolic equations in simple convex polytopes with time irregular coefficients. SIAM J. Math. Anal., 46 (2014), no.3, 1789–1819.
- Hongjie Dong and Doyoon Kim. Schauder estimates for a class of non-local elliptic equations. DCDS-A, 33 (2013), no.6, 2319–2347.
- Hongjie Dong and Doyoon Kim. The conormal derivative problem for higher order elliptic systems with irregular coefficients. in Recent Advances in Harmonic Analysis and Partial Differential Equations, Contemporary Mathematics, vol. 581, Amer. Math. Soc., Providence, RI, 2012, pp. 69–97.
- Doyoon Kim. Global regularity of solutions to quasiliner conormal derivative problem with controlled growth. J. Korean Math. Soc., 49 (2012), No.6, 1273–1299.
- Hongjie Dong and Doyoon Kim. On
 -estimates for a class of non-local elliptic equations. JFA, 262 (2012), no.3, 1166–1199.
-estimates for a class of non-local elliptic equations. JFA, 262 (2012), no.3, 1166–1199.
- Hongjie Dong and Doyoon Kim. Global regularity of weak solutions to quasilinear elliptic and parabolic equations with controllable growth. CPDE, 36 (2011), no.10, 1750–1777.
- Hongjie Dong and Doyoon Kim. Higher order elliptic and parabolic systems with variably partially BMO coefficients in regular and irregular domains. JFA, 261 (2011), no.11, 3279–3327.
- Hongjie Dong and Doyoon Kim. Parabolic and elliptic systems in divergence form with variably partially BMO coefficients. SIAM J. Math. Anal., 43 (2011), no.3, 1075–1098.
- Hongjie Dong and Doyoon Kim. On the
 -solvability of higher order parabolic and elliptic systems with BMO coefficients. Arch. Ration. Mech. Anal., 199 (2011), no.3, 889–941.
-solvability of higher order parabolic and elliptic systems with BMO coefficients. Arch. Ration. Mech. Anal., 199 (2011), no.3, 889–941.
- Hongjie Dong and Doyoon Kim.
 solvability of divergence type parabolic and elliptic systems with partially BMO coefficients. CVPDE, 40 (2011), no.3-4, 357–389.
solvability of divergence type parabolic and elliptic systems with partially BMO coefficients. CVPDE, 40 (2011), no.3-4, 357–389.
- Doyoon Kim. Parabolic equations with partially BMO coefficients and boundary value problems in Sobolev spaces with mixed norms. Potential Analysis, 33 (2010), no.1, 17–46.
- Hongjie Dong and Doyoon Kim. Elliptic equations in divergence form with partially BMO coefficients. Arch. Ration. Mech. Anal., 196 (2010), no.1, 25–70.
- Hongjie Dong and Doyoon Kim. Parabolic and elliptic systems with VMO coefficients. Methods Appl. Anal., 16 (2009), no.3, 365–388.
- Doyoon Kim. Elliptic and parabolic equations with measurable coefficients in
 -spaces with mixed norms. Methods Appl. Anal., 15 (2008), no.4, 437–468.
-spaces with mixed norms. Methods Appl. Anal., 15 (2008), no.4, 437–468.
- R.M. Balan and Doyoon Kim. The stochastic heat equation driven by a Gaussian noise: Markov property. Commun. Stoch. Anal., 2 (2008), no.2, 229–249.
- Doyoon Kim. Elliptic equations with nonzero boundary conditions in weighted Sobolev spaces. J. Math. Anal. Appl., 337 (2008), no.2, 1465–1479.
- Doyoon Kim. Trace theorems for Sobolev-Slobodeckij spaces with or without weights. J. Funct. Spaces Appl., 5 (2007), no.3, 243–268.
- Doyoon Kim. Parabolic equations with measurable coefficients II. J. Math. Anal. Appl., 334 (2007), no.1, 534–548.
- Doyoon Kim and N.V. Krylov. Parabolic equations with measurable coefficients. Potential Analysis, 26 (2007), no.4, 345–361.
- Doyoon Kim and N.V. Krylov. Elliptic differential equations with coefficients measurable with respect to one variable and VMO with respect to the others. SIAM J. Math. Anal., 39 (2007), no.2, 489–506.
- Doyoon Kim. Second order elliptic equations in
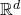 with piecewise continuous coefficients. Potential Analysis, 26 (2007), no.2, 189–212.
with piecewise continuous coefficients. Potential Analysis, 26 (2007), no.2, 189–212.
- Doyoon Kim. Second order parabolic equations and weak uniqueness of diffusions with discontinuous coefficients. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), 5 (2006), no.1, 55–76.
- Doyoon Kim. Partial differential equations in Sobolev spaces with or without weights. PhD thesis, University of Minnesota, 2005.
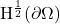 for Boundary Data. Submitted.
for Boundary Data. Submitted. -estimates of the conormal derivative problem for parabolic equations with time measurable coefficients and
-estimates of the conormal derivative problem for parabolic equations with time measurable coefficients and 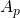 -weights. Submitted.
-weights. Submitted. -estimates for parabolic equations in divergence form with a half-time derivative. (https://authors.elsevier.com/a/1lH0Z_W4cPkNh) JDE, 443 (2025), 113560.
-estimates for parabolic equations in divergence form with a half-time derivative. (https://authors.elsevier.com/a/1lH0Z_W4cPkNh) JDE, 443 (2025), 113560. -estimates for non-local equations. CVPDE, 62 (2023), no.2, Paper No.62, 28 pp.
-estimates for non-local equations. CVPDE, 62 (2023), no.2, Paper No.62, 28 pp. -estimates for time fractional parabolic equations in divergence form with measurable coefficients. JFA, 278 (2020), no.3, 108338, 66 pp.
-estimates for time fractional parabolic equations in divergence form with measurable coefficients. JFA, 278 (2020), no.3, 108338, 66 pp.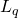 -estimates for stationary Stokes system with coefficients measurable in one direction. (http://rdcu.be/GCJ1) Bull. Math. Sci., 9 (2019), no.1, 1950004, 30 pp.
-estimates for stationary Stokes system with coefficients measurable in one direction. (http://rdcu.be/GCJ1) Bull. Math. Sci., 9 (2019), no.1, 1950004, 30 pp.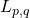 -estimates for higher order elliptic and parabolic systems with BMO
-estimates for higher order elliptic and parabolic systems with BMO coefficients on Reifenberg flat domains. (https://rdcu.be/bAY4C) CVPDE, 58 (2019), no.3, Paper No.90, 29 pp.
coefficients on Reifenberg flat domains. (https://rdcu.be/bAY4C) CVPDE, 58 (2019), no.3, Paper No.90, 29 pp. -estimates for time fractional parabolic equations with coefficients measurable in time. Adv. Math., 345 (2019), 289–345.
-estimates for time fractional parabolic equations with coefficients measurable in time. Adv. Math., 345 (2019), 289–345. -estimates for elliptic and parabolic equations with
-estimates for elliptic and parabolic equations with 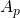 weights. Trans. Amer. Math. Soc., 370 (2018), no.7, 5081–5130.
weights. Trans. Amer. Math. Soc., 370 (2018), no.7, 5081–5130.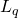 -estimates for stationary Stokes system with partially BMO coefficients. JDE, 264 (2018), no.7, 4603–4649.
-estimates for stationary Stokes system with partially BMO coefficients. JDE, 264 (2018), no.7, 4603–4649. coefficients in weighted Sobolev spaces. DCDS-A, 36 (2016), no.9, 4895–4914.
coefficients in weighted Sobolev spaces. DCDS-A, 36 (2016), no.9, 4895–4914.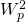 estimates for elliptic equations with piecewise constant coefficients. JFA, 267 (2014), no.10, 3963–3974.
estimates for elliptic equations with piecewise constant coefficients. JFA, 267 (2014), no.10, 3963–3974. -estimates for a class of non-local elliptic equations. JFA, 262 (2012), no.3, 1166–1199.
-estimates for a class of non-local elliptic equations. JFA, 262 (2012), no.3, 1166–1199. -solvability of higher order parabolic and elliptic systems with BMO coefficients. Arch. Ration. Mech. Anal., 199 (2011), no.3, 889–941.
-solvability of higher order parabolic and elliptic systems with BMO coefficients. Arch. Ration. Mech. Anal., 199 (2011), no.3, 889–941. solvability of divergence type parabolic and elliptic systems with partially BMO coefficients. CVPDE, 40 (2011), no.3-4, 357–389.
solvability of divergence type parabolic and elliptic systems with partially BMO coefficients. CVPDE, 40 (2011), no.3-4, 357–389. -spaces with mixed norms. Methods Appl. Anal., 15 (2008), no.4, 437–468.
-spaces with mixed norms. Methods Appl. Anal., 15 (2008), no.4, 437–468.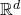 with piecewise continuous coefficients. Potential Analysis, 26 (2007), no.2, 189–212.
with piecewise continuous coefficients. Potential Analysis, 26 (2007), no.2, 189–212.