여러 가지로 나누어 토론하기 바래요. 글을 쓰면 글 끝머리에 자신의 이름을 꼭 쓰세요.(날자 시간도 쓰세요.)
헉..아무도 글을 안올린다… 교수님..힌트라도 주시면 안되나요? 힌트는 책의 문제와 같이 우선 몇 가지 특수한 경우에 세 보는 거예요. – 김영욱
- 어제 수학과 체육대회 후에 몇 가지 문제에 대하여 이야기 했어요. 이 문제에는 힌트를 주려고 해도 별로 할 말이 없는데 우선 거울 사이의 각이 특수각일 때를 생각해 보는 것이지요. 적어도 60도나 90도를 그려보고 그 다음에 이 사이의 각(70도 같은)을 생각해 보면 어떻게 될지는 예측할 수 있어요. 그 다음에는 왜 그렇게 될 수 밖에 없는지 생각해 보는 것이지요.
- 시간중에 이야기했던 복잡한 부분, 예를 들어 반쪽짜리 촛불 등, 같은 것은 위의 문제를 다 푼 다음에 생각해 볼 조그만 재미일 뿐입니다.
아래 올려준 것은 그럴 듯 하네요. 정확한지는 확인해 보지 않았지만. 그런데 $ ∠ B$ 의 크기에 따라 상의 개수가 변하는 것은 왜 그런지 확실히 설명할 수 있지 않나요?
교수님, 시간이 많이 지나서 저도 기억이 나지 않습니다. 이제서야 질문에 답하기 위해 다시 그림을 들여다 보니 저또한 무슨 말을 적어 놓았는지 이해하지 못하겠습니다. 설명없이 그림만 올려놓은 제가 무성의 했다고 느껴집니다.
음, 대략적으로 설명하면 그림 3.1과 3.2를 보면 각이 50도 일때 B의 위치에 따라서 상의 개수가 7개도 되고 8개도 되었습니다. 그래서 각B를 조금씩 움직여 가며 그림을 그려보고 또, 두 거울사이의 각을 다르게 설정하여 각B의 위치를 조금씩 움직이면서 상의 개수가 달라지는 각B를 구한 뒤 나중에 종합하여 아래의 식을 만들었습니다.
이제 다시 생각해보니 어딘가 이상한게 괜히 망신만 당하는게 아닌지 모르겠습니다. 죄송합니다. 2004160085 이동선 2006/12/04 17:30
2006/10/20 20:30 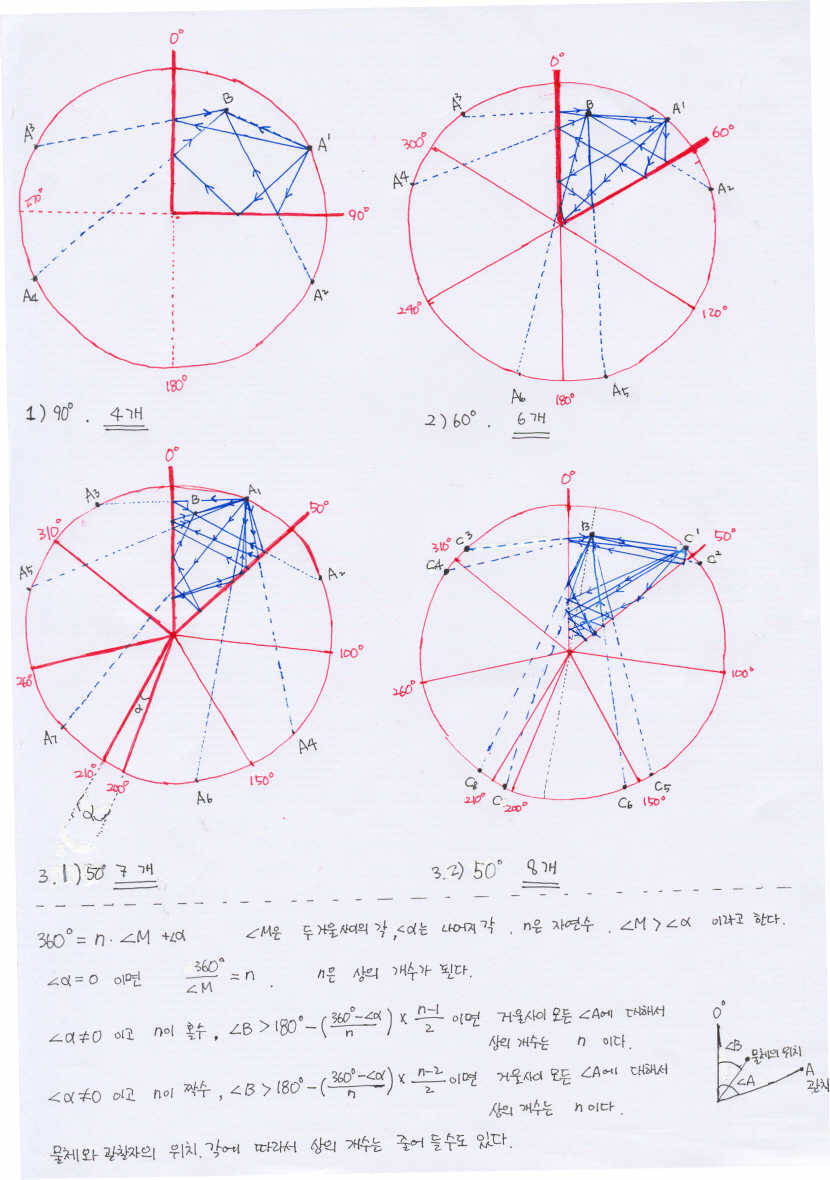
무작정 그리고 엄밀히 생각안해봐서 맞는지 틀린지 모르겠음 (보완할 것고 많고) ^-^;;; 2004160085 이동선