[wiki:MyMisc 위로]
(TableOfContents)
보이지 않는 것을 보기 위하여
포앙카레는 고차원을 보았는가
Computer Graphics가 유행한다고 한다. Algorithm을 바탕으로 하여 자동적으로 생성되는 도형은, 때로는 예술가가 만드는 것보다 신비적 매력이 있다. 그런데 그러한 도형과 같을 정도, 또는 한층 더 신비적인 도형을 수학자는 오랜 동안 연구해왔다. (새삼스럽게 또라고 말씀하실지 모르지만) 고차원의 도형을 말하는 것이다. 우선, 과연 수학자는 고차원의 도형을 “보고” 있는지에 대하여 써보고 싶다.
포앙카레의 “과학과 방법”의 가운데, 공간인식에 관하여 쓰여진 부분이 있다. 포앙카레의 결론은, 간단하게 말하면 삼차원 공간에 있어서 생활한 경험(결국 자기가 공간 내에서 운동한, 그것이 시각과 촉각이 결합된 경험)이 공간인식을 만드는 것 같다고 생각한다. 이것과 칸트의 선험적 인식 운운과의 관계 등을 논한 철학자도 있는 것 같다.
그러하지만 포앙카레가 이것을 쓴 당시, 틀림없이 고차원의 기하학의 중심이 될만한 수학, 즉, 위상기하학을 건설중이었다는 것을 철학자들이 알고 있었는지 어땠는지는 뚜렷하지 않다.
포앙카레에 있어서, 예컨대 4차원의 공간이 과연 “보이”는가라는 것은 인식론의 문제라기보다, 고차원의 기하학을 어떻게 해서 건설할 것인가라는 실제적인 문제였을 것이다. 그 결론이 이러한 것이었다고 하면 포앙카레로 하여금 결국 4차원은 “보이지 않았다”라고 해야할지 모른다.
도형적 직감
佐藤幹夫씨는 어떤 대담 가운데서 원(圓)의 인식에 언급하여, 원을 이해하려면 ” $ x^2 + y^2= 1$ ” 이라는 방정식에 의하는 것이 결국 제일 좋다”라고 강조하고 계시다. 위대한 佐藤선생에게 거역하는 것은 분수를 대단히 넘는 일이지만 기하학자로서는, 원이 지니는 도형적 이미지의 면을 방정식보다 소중하게 여기고 싶다. 머리 속에 그려진 둥근 이미지야말로 원이라고 생각하고 싶다.
인간의 뇌 가운데 시각에 관한 부분은 대단히 많고, 시각을 통하여서의 인식은 인간이 물건을 생각하는 중심에 위치한다고 한다. 수학에 있어서도 도형적 직감은 사물을 인식하는 가장 명쾌한 방법이다. 예를 들면, 논문에서는 긴 식으로 설명이 되어있어 이해가 곤란한 것을, 연구집회 같은 곳에서 저자가 그림을 하나 그린 찰나, 곧 알 수 있다는 것은 쉽게 경험할 수 있는 일이다.
그러한 의미에서는, 고차원의 도형을 연구할 때 사용하는 것도 역시 도형적 직감이다. 그렇다고 하면 100년 가까운 수학의 진보는 포앙카레에게 보이지 않았던 고차원의 도형을 보는 것을 가능하게 했을까?
답은 예스이기도 하고 노우이기도 하다. 만일 본다는 것을 보통 우리들이 (눈으로) 물건을 본다. 또는 본 일이 있는 어떤 물건을 생각해 묘사하는, 그런 의미라면, 포앙카레보다 잘 “보이는” 수학자들은 그리 많지 않다. 그러나 현재 한창 연구되고 있는 고차원의 기하학은 도형적 직감 없이는 있을 수 없다.
Exotic한 구면
예를 들면, exotic한 구면이라는 것을 아는가? 정확히는 7차원 구면과 위상동형이지만, 미분동형은 아닌 도형이다. (위상동형이라든가 미분동형이라는 것은 여기서는 설명하지 않는다. 무엇인가 구라는 보통 것 같으면서 그것과는 다른 것이 7차원에는 있다고 생각하면 된다.) 이것에 관하여 서술한 Milnor의 논문은 짧으므로, 위상기하학의 전문가라면 누구든지 Milnor가 행한 구성을 전체적으로 이해할 수 있다. 그러나 그렇게 해서 만들어진 도형 전체를 눈으로 본 것 같이 생각하고 그려서, 그것이 7차원 구면과 위상동형이기는 하나 미분동형은 아닌 것을 시각적으로 납득하는 것은, 적어도 필자에게는 불가능하다. 그러면 수학자는 어떻게 그것을 이해하고, 그래도 거기에 기하학적 직감을 사용할 수 있는 것인가?
우선, 좀 더 쉬운 예를 들어 말해보자. 평면 위에 두 줄의 직선이 있으면, 그것은 (평행하지 않은 한) 한 점에서 교차한다라고 하는 것은 물론 독자는 잘 알 것이다. 그러면 (3차원)공간의 두 직선이면 어떨까? 물론 이 책의 독자는 일반적으로 공간의 두 직선은 교차하지 않는 것을 알고 있고, 그것을 나타내는 그림을 머리로 생각하며 그릴 수도 있겠지만, 예를 들어 수학을 잘 못하는 중학생에게 이것을 질문하면, 정답률은 100%에서 어느 정도 떨어질 것이다. 그러나 누구에게라도 3차원 공간 안에 두 줄의 직선이 그어진 그림을 보여주면 이것을 이해할 것이다. 그리하여 그것을 납득하면 다음부터는 그 그림을 자기 혹자서도 머리속에서 생각하여 떠올릴 수 있을 것이다.
4차원의 도형적 직감의 쉬운 한가지 예
이것은 간혹 3차원의 문제로, 실제로 그림으로 그려진다. 그러면 4차원공간 가운데의 두 개의 (2차원)평면이면 어떨까? 이것을 처음 들으면 우선 망설일 것이다. 아마 많은 사람에게는 그림을 생각해내서 직접 답을 내는 일을 즉시는 못하기 쉬울 것이다.
여기서 식을 사용할 필요가 있다. 즉 4차원 공간 중의 평면이란 4변수의 두 줄의 연립1차 방정식의 해이며, 이 것은 보통 단 하나 존재한다. 이렇게 해서 4차원공간 중의 두 개의 평면이 보통은 한 점에서 교차하는 것을 알며, 그러면 다음부터는 4차원에서 두 개의 평면이 한 점에서 교차하는 그림이 어쩐지 머리 속에 그려질 것 같아진다.
Exotic한 구면을 만든다
이 것이 제 1단계이다. 이 것은 보여지고 있다고 하여도 좋을 것이다. 그러나 많은 문제에서는 이와 같이 “보여지고 있다”는 고찰만으로는 끝나지 않는다. “보이는” 것은 전체 상(像) 중의 그저 명색뿐인 일부분에 지나지 않는다. 예를 들면, 처음에 쓴 exotic한 구면의 경우를 생각하자. 이것을 만드는 한가지 방법은 다음과 같다.
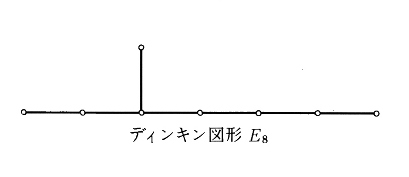
우선 딘킨도형 E_8을 생각한다.이것이 무엇인지 설명은 안 해도 이것은 그래프니가 분명히 눈으로 볼 수 있다. 다음에 4차원 구면의 접bundle을 여덟 개의 딘킨도형에 따라 펴 합한다. (따라서 편다는 의미도 생략한다.) 4차원 구면의 접bundle이라 함은 8차원의 도형으로 4차원 구면에 두께를 더한 것이라고 생각하면 된다. 이것은 앞서 말한 4차원 중에서 두 개의 평면이 한 점에서 교차하는 것이 “보인다”라는 의미에서라면 보인다. 그것으로 생긴 도형도 뭔가 보인다는 것에 속한다. Exotic한 구면은 이 도형의 경계이다.
여기까지 오면 적어도 필자에게는 이것이 구면과 위상동형이라는 것은 “한눈에”는 알 수 없다. 더욱이 이것이 구면과 미분동형이 아니라는 것의 증명이라하면, 눈으로 본다는 것은 가능하다고는 생각하지 않는다. 물론 그 증명의 각각의 스텝은 도형적 직관에 따라 “보인다”. 그러나 그것들의 스텝은 이론으로 결부시켜져 있고, 전체는 그림으로 이해하였다고는 도저히 말할 수 없다.
본다는 것의 새로운 바람직한 자세
이 설명으로 이해되었는지 어떤지 자신은 없지만, 한가지 강조해 놓고 싶은 것은, 수학의 엄밀성과 추상성이 이 과정에서 불가결하다는 것이다. 수학 이외의 세계에서 무엇을 논할 때, 우리들은 단지 삼단논법만을 따라서 옳은 것을 이해하는 것은 아니다. 각 단계에서 주장되고 있는 일이 경험에 비추어서 납득하기 어려우면, 어떤 방법으로 논리를 납득하여도 그 결론은 거부할 것이다. 그러나 수학의 세계에서는 자주 그 각 단계에서의 정당성의 지침이 되는 경험이 결여되어있다. 시각적 직감으로 아는 것은 부분상(像)에 불과하다. 직감을 잃었을 때 사용되는 것은 논리밖에 없다. 그러나 그렇게 해서 엄밀한 증명을 통하여 많은 사실을 집적하였을 경우, 최후에 몇 개의 도형적 직감(어떤 것은 직접 시각적이고, 어떤 것은 그렇지 않은)이 얻어진다. 그리하여 이해가 깊어져가는 것을 보여져간다고 한다면, 우리들은 고차원을 보고 있다고 해도 좋을 것이다.
지난주 연구실을 청소하다, 고교생 때 읽던 책이 몆 권 나왔다. 상대성이론이라든가 우주론이라든가 하는 계몽서와 더불어, 사차원 공간이라든가 뭔가가 (다소 애교스럽게) 써있는 책도 있다. 당시 수학을 공부하면 차원이 높은 공간이 눈에 보일 것이라고 동경하고 있던 일이 생각난다. 그 기대는 저버렸다. 결국, 기하학의 전문가가 되어도 4차원의 도형을 눈으로 본 것 같이 생각해 그리지는 못한다. 그러나 그 대신, 본다는 것의 새로운 바람직한 자세는 알았다. 상상력과 논리의 결합에 따라 보이지 않는 것을 본다는 것. 이것은 대단한 일이 아니라고 하겠는가?