SageMath로 Costa 곡면 그리기

by

양성덕
20210413

세 번째 시도 당시 알지 못했던 기법을 알게 되서 이제 다음과 같이 그림을 완성한다. 이러면 Weber가 그린 방법을 그대로 따른 셈이 된다.

참고 문헌
[2] Matthias Weber, Costa’s Minimal Surface, Mathematica Notebook File

%display latexIn [1]:

var('rho')

rho = ( gamma(3/4)/sqrt(2)/gamma(5/4) ).n()

In [2]:

Phi1(w) = 2*rho*I*sqrt(w)*hypergeometric((1/4,3/2,), (5/4,), w^2)
Phi2(w) = -2/(3*rho)*I*w*sqrt(w)*hypergeometric((1/2,3/4,), (7/4,), w^2)

In [3]:

omega1(z) = -1/2*( Phi1(z) - Phi2(z))
omega2(z) =  I/2*( Phi1(z) + Phi2(z))
omega3(z) =  1/2*log(-1+z) - 1/2*log(1+z)

In [4]:

F(z) = ( omega1(z).real(), omega2(z).real(), omega3(z).real() )

In [5]:

p(w) = sqrt( 1 + exp(w) )

In [6]:

var('y');

In [7]:

points = [(p(x+I*y).real(), p(x+I*y).imag()) for x in srange(-1,3,0.1) for y in srange(0*pi, pi, 0.05*pi, include_endpoint=True)]

In [8]:

list_plot(points, aspect_ratio=1)

Out[8]:

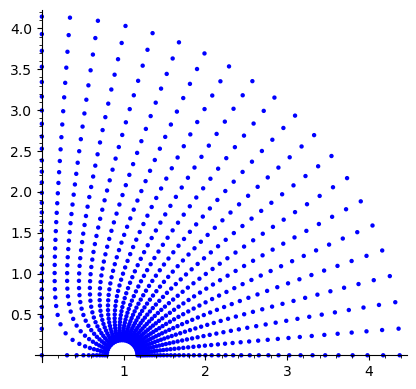
In [9]:

xlist=  [-3.5,-3.0,-2.5, -2.0,-1.5, -1.0,-0.5,-0.3,-0.2,-0.1,-0.05,-0.03,0.0,0.03,0.05,0.1,0.2,0.4,0.6,0.8,1.0,1.2,1.5,2.0 ,2.5,3.0 ,3.5,4.0,5.0,6.0 ];
xlen= len(xlist);


ylist= list(pi*vector([0.001,0.05,0.08,0.16,0.24,0.32,0.4,0.48,0.56,0.64,0.72, 0.8,0.88,0.95,0.98,0.99,1.0]));
ylen=len(ylist);

In [10]:

var('x y');

In [11]:

X = lambda x: xlist[ int(round(x)) -1] if x<0.5 or x>xlen + 0.4 else xlist[ int(round(x)) -1]
Y = lambda y: ylist[ int(round(y)) -1] if y<0.5 or y>ylen + 0.4 else ylist[ int(round(y)) -1]

In [12]:

f = (lambda x,y: omega1(p(X(x)+ I*Y(y))).real(), 
     lambda x,y: omega2(p(X(x)+ I*Y(y))).real(),
     lambda x,y: omega3(p(X(x)+ I*Y(y))).real()
     )
gr1 = parametric_plot3d( f, (x, 1,xlen),(y,1,ylen))

In [13]:

gr1.show(frame=False)

한 조각에서 전체 그리기

이제 곡면을 변환한다. 우리가 원하는 변환은⎛⎜⎝xyz⎞⎟⎠→⎛⎜⎝yx−z⎞⎟⎠=⎛⎜⎝01010000−1⎞⎟⎠⎛⎜⎝xyz⎞⎟⎠=⎛⎜⎝−10001000−1⎞⎟⎠⎛⎜⎝0−10100001⎞⎟⎠⎛⎜⎝xyz⎞⎟⎠(1)(1)(xyz)→(yx−z)=(01010000−1)(xyz)=(−10001000−1)(0−10100001)(xyz)

마지막에 나타난 바와 같이 행렬을 분해한 이유는, 소스 코드까지 들여다 보아도 회전과 scaling을 적용하는 방법은 알겠는데 일반적 선형변환을 적용하는 방법은 알아낼 수가 없어서다.In [14]:

gr2 = gr1.transform(rot=(0,0,1,pi/2)).transform(scale=(-1,1,-1))

그런데 해 보면

gr1.transform(rot=(0,0,1,pi/2)).transform(scale=(-1,1,-1))

도 같은 결과를 주는 것 같다. 확실한 결과는 모르겠다.

참고로 위 변환을 알아낸 방법은 다음과 같다.

  • dir(gr1)로 모든 attributes와 methods를 알아내고자 했으나 실패.
  • type(gr1)로 나오는 a의 클래스 이름과 그 내용이 정의되어 있는 소스 파일 위치 파악
  • 해당 위치로 가 소스 파일 읽다가 위 내용을 알게 됨.

In [15]:

type(gr1)

Out[15]:

<class 'sage.plot.plot3d.parametric_surface.ParametricSurface'>

In [16]:

gr12 = gr1.transform(scale=(-1,1,1))
gr13 = gr1.transform(scale=(-1,-1,1))
gr14 = gr1.transform(scale=(1,-1,1))

gr22 = gr2.transform(scale=(-1,1,1))
gr23 = gr2.transform(scale=(-1,-1,1))
gr24 = gr2.transform(scale=(1,-1,1))

gr = gr1 + gr2 + gr12 + gr13 + gr14 + gr22 + gr23 + gr24

In [17]:

gr.show(frame=False)

참고) 이 파일을 html 파일로 변환할 때 displayed equation을 그것만 따로 한 markdown 셀에 넣지 않으면 변환이 제대로 되지 않는다.

Leave a Comment