다음 문제는 오랫동안 (2021년 10월 현재 약 7년?) 저를 괴롭히는 문제입니다. 혹시 아무라도 좋은 해법을 알려주면 감사하겠습니다.
문제) 공간의 좌표를 $xyt$로 나타내자. 이변수 함수 $t=f(x,y)$에 대한 다음 편미분방정식의 수치해를 구하여라.
$$
(1- f_{y}^2) f_{xx} + 2 f_x f_y f_{xy} + (1-f_{x}^2) f_{yy} =0, \qquad 0 \le x,y \le 1.
$$
단 둘레조건은 다음과 같다. 모든 $s \in (0,1)$에 대하여
$$
f(s,0) = f(s,1) = 0, \quad f(0,s) = f(1,s)=1
$$
이 함수는 3차원 로렌쯔 공간의 한 0평균곡률곡면을 나타낸다.
참고 2) 이 문제의 해는 존재하나 유일한 지, 안정적인지는 잘 모릅니다. 존재하는 해는 다음 논문에 있습니다.
[1] Shoichi Fujimori, Wayne Rossman, Masaaki Umehara, Kotaro Yamada, & Seong-Deog Yang, Embedded Triply Periodic Zero Mean Curvature Surfaces of Mixed Type in Lorentz-Minkowski 3-Space, Michigan Math. J. 63 (2014), 189–207, 8쪽 그림 8, 9.
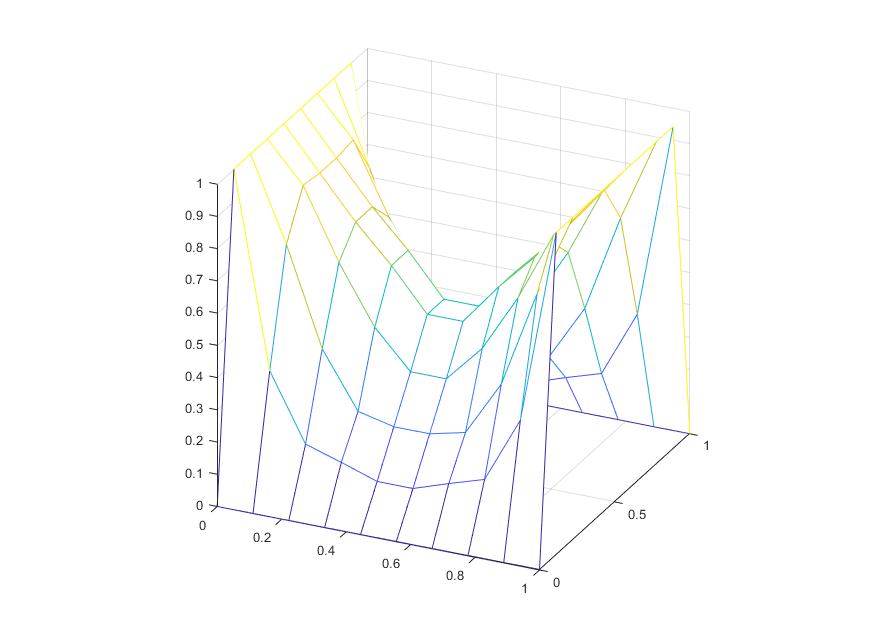
저작원 문제로 그림을 올려도 되는지 잘 몰라서 논문에 있는 그림은 안 올립니다. 다음은 김준석 교수님이 시도하신 해입니다. 그물눈의 크기를 더 줄이면 그림이 터진다고 하시네요. 즉, 매끄러운 곡면을 얻을 수 없었습니다. 참, 이 PDE는 타원형과 쌍곡형이 섞여있는 편미분방정식입니다.
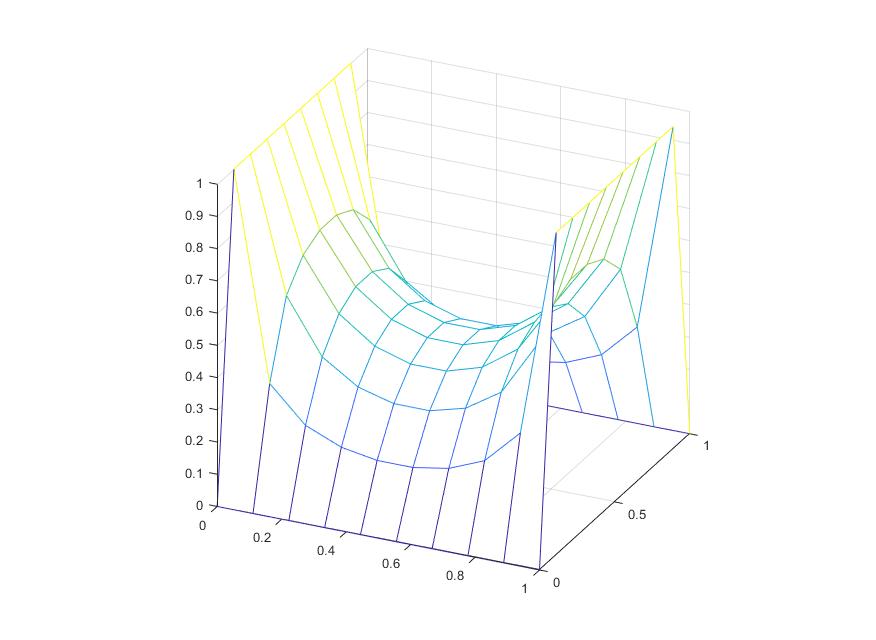
참고 1) 이 문제에 대한 유클리드 공간 버전은 다음과 같다.
공간의 좌표를 $xyz$로 나타내자. 이제 이 이변수 함수 $z=f(x,y)$에 대하여 다음 함수의 수치해를 구하여라.
$$
(1+ f_{y}^2) f_{xx} – 2 f_x f_y f_{xy} + (1+f_{x}^2) f_{yy} =0, \qquad 0 \le x,y \le 1.
$$
단 둘레조건은 다음과 같다. 모든 $s \in (0,1)$에 대하여
$$
f(s,0) = f(s,1) = 0, \quad f(0,s) = f(1,s)=1
$$
이 함수는 3차원 유클리드 공간의 한 극소곡면을 나타낸다.